There is a positive integer in each square of a rectangular table. In each move, you may double each number in a row or subtract 1 from each number in a column. Can you arrive to a situation where there are only zeros on the table? How Should These Kind Of Problems Be Approached In […]
Tag: Combinatorics
A Problem From Stanford Mathematics Tournament 2008 (Team Test)
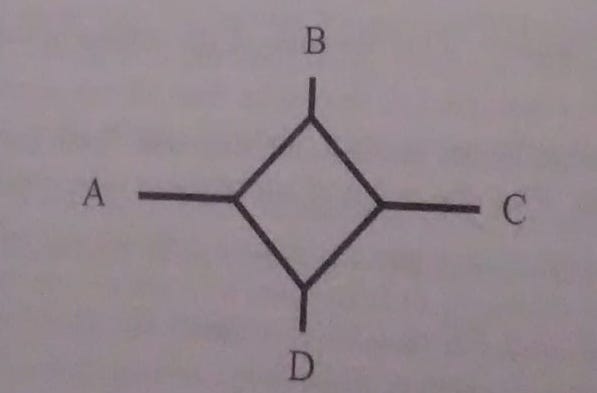
Daphne is in a maze of tunnels shown below. She enters at A, and at each intersection, chooses a direction randomly (including possibly turning around). Once Daphne reaches an exit, she will not return into the tunnels. What is the probability that she will exit at A? The Idea At first, I will denote by […]
Old Problem With Generating Functions
A similar problem to this one is the one that initiated me to the art of using the generating functions, I’ll tell you a version which has less calculations to make. If you roll a complete set of DnD dice, in how many ways can you obtain 13 as sum of their results? Just for […]
Double Counting: Part 1
Double counting is a widely used technique of combinatorics, which consists of counting the same quantity with two different methods so that you can create an equation. Today I’m going to show you some of its application. Double Counting In A Polyhedron Does a polyhedron exist with an odd number of faces each having an […]
Two Examples For The Box Principle
The box principle is a pretty simple yet so useful mathematical principle which asserts: If there are n+1 objects to put into n boxes, then 2 objects must be in the same box. This makes us think that usually we just have to divide our set of possibilities in mutually exclusive boxes and prove that […]
An Insight Into Generating Functions
The technique of using a generating function is widely used in combinatorics: you have a polynomial where the coefficient of the term of degree n represents how many times n appears in your counting problem. Let’s see a simple example to make it clearer. Let’s say we have 2 standard dice, we roll both and […]