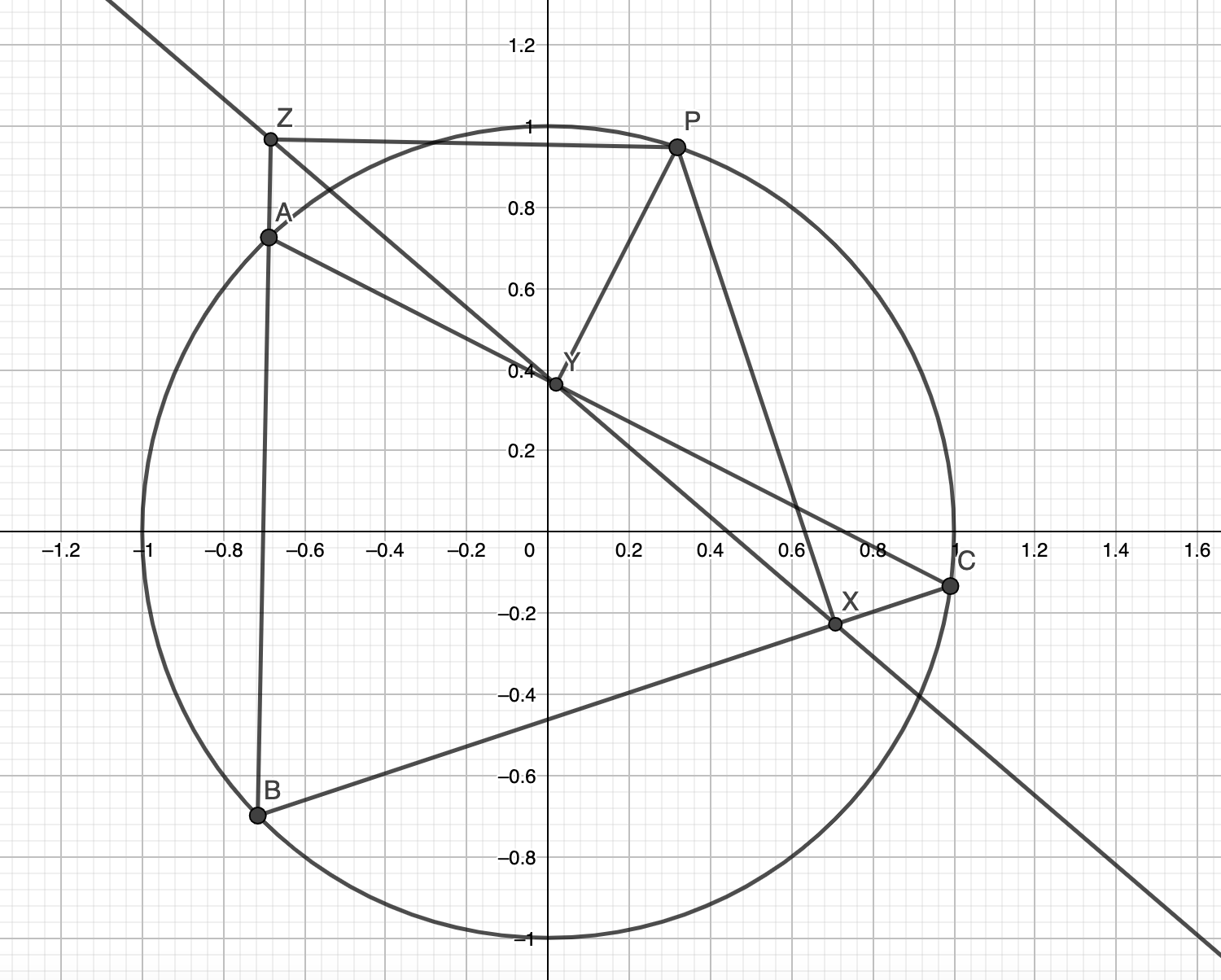
Given a point P on a triangle’s ABC’s circumcircle, then its projections on the sides of ABC are collinear (Simson Line). Using the notation from the figure above, notice that perpendiculars produce cyclic quadrilaterals: P is on the circumcircle of triangles YZA, ZXB and XYC. So we compute: due to all the cyclic quadrilaterals, and […]
Category: Maths
Double Counting: Part 1
Double counting is a widely used technique of combinatorics, which consists of counting the same quantity with two different methods so that you can create an equation. Today I’m going to show you some of its application. Double Counting In A Polyhedron Does a polyhedron exist with an odd number of faces each having an […]
Old But Gold Polynomials
This article is about a couple of problems about polynomials which I regard as highly instructive. Seems A Demon But It’s Really Not I first saw this problem in 2018, and I initially thought it was a very hard problem, except it wasn’t. But, at first sight, it could make you feel a bit lost. […]
Cauchy-Schwarz And Titu Inequalities
Today I’m going to show two very nice inequalities to know, which really are useful in the mathematical olympiads. What They Say And Their Proof The Cauchy-Schwarz inequality asserts that, for real tuples we have: Here’s the proof: consider the expression It’s obviously true since each term of the sum is non negative. Hence we […]
Great Classic: Hanoi Tower
Tower of Hanoi consists of three pegs or towers with n disks placed one over the other. The objective of the puzzle is to move the stack to another peg following these simple rules. Only one disk can be moved at a time. No disk can be placed on top of the smaller disk. In […]
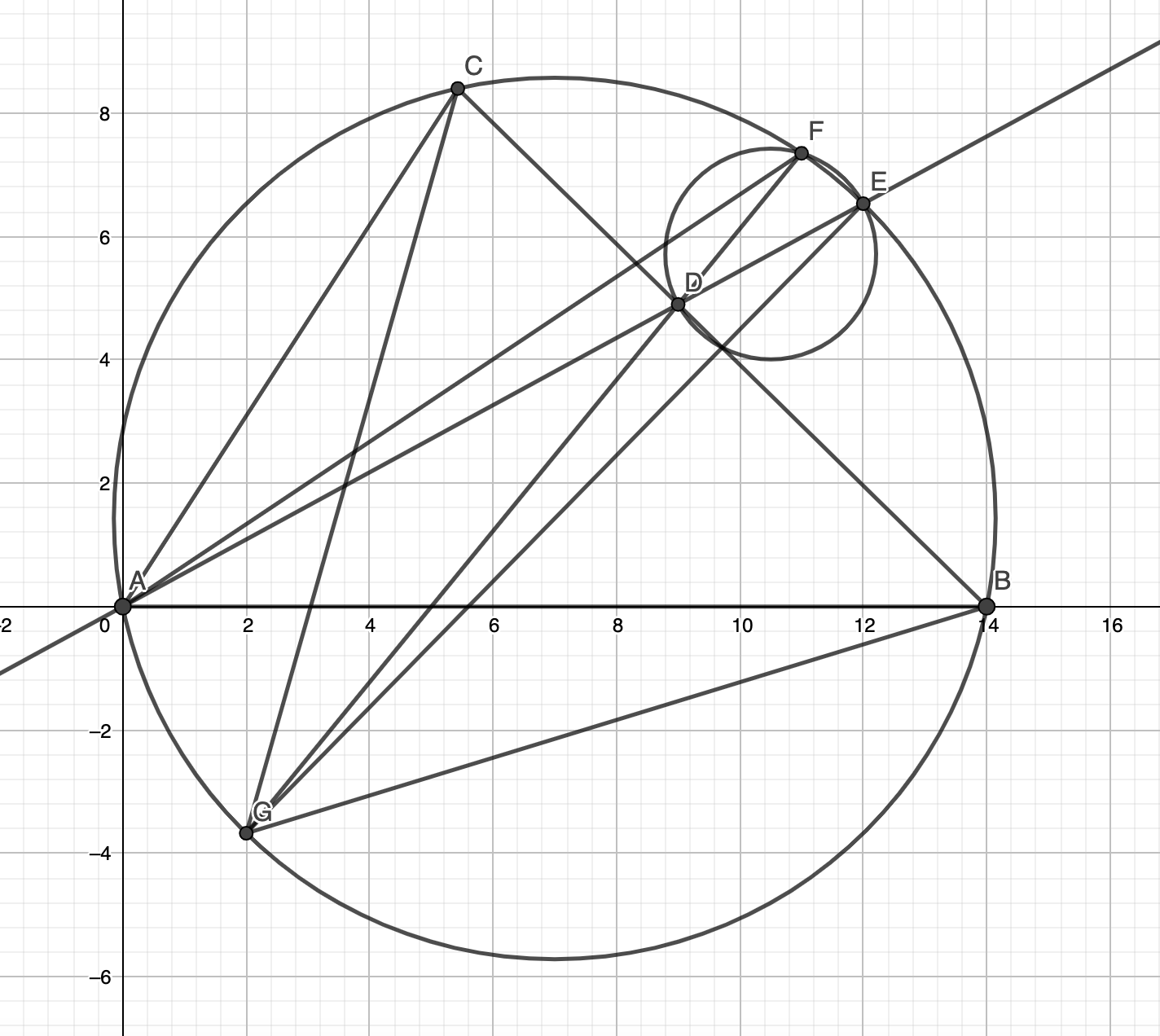
Sometimes Geometry Just Needs Smart Calculations
In the figure, suppose AB = 14, BC = 12, CA = 10. AD is the angle bisector of A, intersecting the circumcircle of ABC at E. The circle with diameter DE intersects the circumcircle of ABC again at F. Find the measure of AF squared. To solve this problem, I used a theorem named […]
Two Examples For The Box Principle
The box principle is a pretty simple yet so useful mathematical principle which asserts: If there are n+1 objects to put into n boxes, then 2 objects must be in the same box. This makes us think that usually we just have to divide our set of possibilities in mutually exclusive boxes and prove that […]
Nice Post-Dinner Diophantine
Today after dinner, I really wanted to do a geometry problem but this diophantine equation just suddenly appeared in front of my eyes and, because it’s been a while since the last number theory problem, I decided to give it a shot. Prove that has no integer solutions. First we notice that the former equation […]
An Old Problem Came To Mind
Two years ago I participated in an online math competition and the problem which was considered as the most difficult was this one: Find Now the trick is finding upper and lower bounds for such quantity. Notice: Similarly If we sum up this relationship for all values we’ll found out it’s telescoping, so we’re left […]
Ellipses And Dilations
I found this problem in the last phase of a team championship I am participating in. We have an ellipse of equation A line through the origin intercepts the ellipse in two points. We draw the tangents to the ellipse at these points and complete the rectangle in such a way that its sides are […]