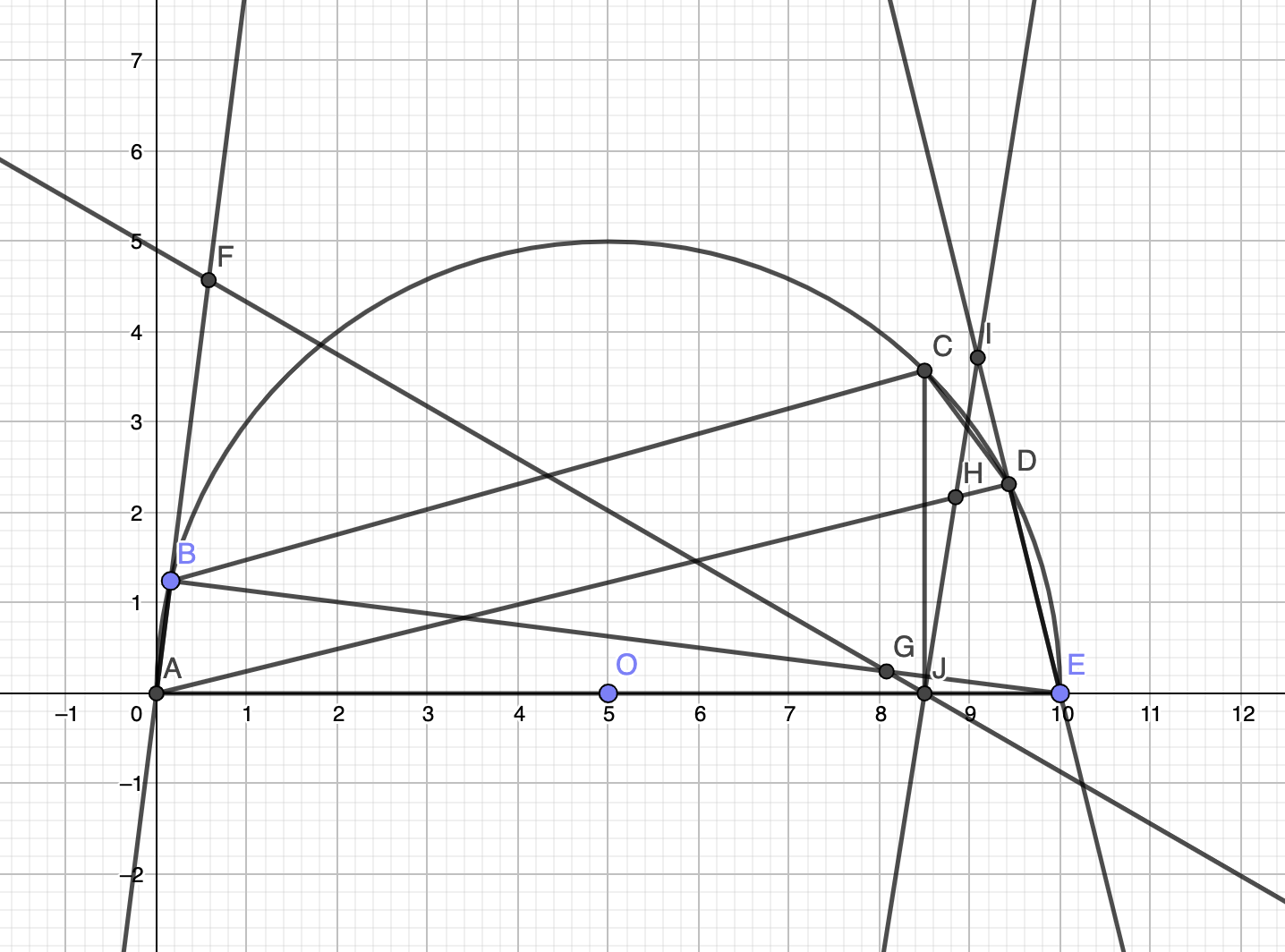
We have a cyclic pentagon, such that AE is a diameter and equals 10. We know and . Now F, G, H, I are the feet of the perpendiculars from C to AB, EB, AD, ED. If FG and HI concur at J, find FJI. Now, let K be the foot of the perpendicular from […]
Category: Geometry
IMO 2007/2
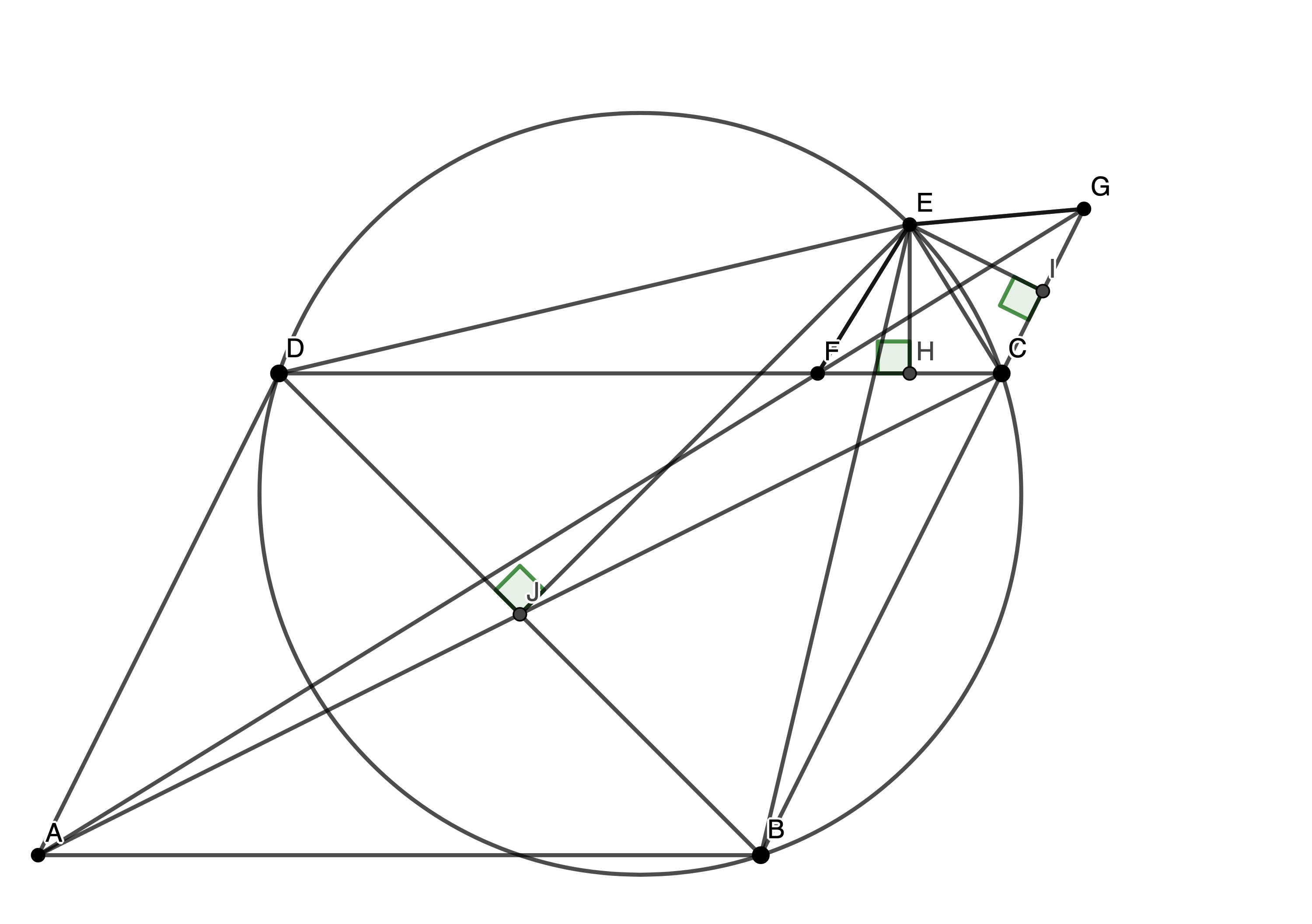
Consider five points A, B, C, D, E such that ABCD is a parallelogram and BCED is a cyclic quadrilateral. Let l be a line passing through A. Suppose that l intersects the interior of the segment DC at F and intersects line BC at G. Suppose also that EF = EG = EC. Prove […]
Shortlist 2001/G1
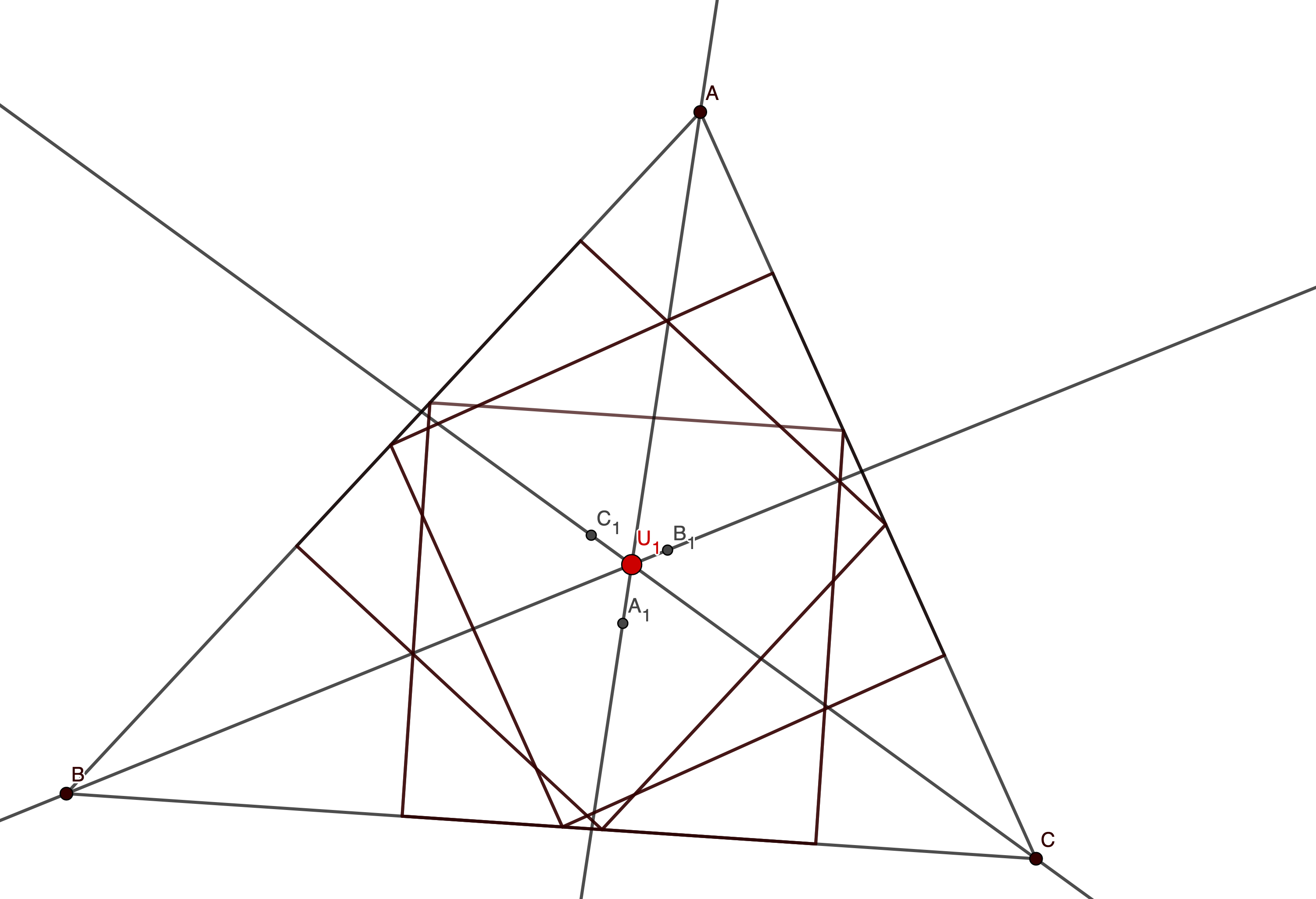
Let be the center of the square inscribed in acute triangle ABC with two vertices of the square on side BC. Thus one of the two remaining vertices of the square is on side AB and the other is on side BC. Points and are defined similarly. Prove that lines and are concurrent. The Idea […]
Euclidean Geometry In Mathematical Olympiads, Evan Chen
The most complete and interesting Geometry theory book I’ve ever read is ‘Euclidean Geometry In Mathematical Olympiads’, by Evan Chen. We could say that it’s the Bible of people who love Geometry problems in the Olympiads. It is divided into 10 theory chapters, which talk about different branches and techniques you can use to solve […]
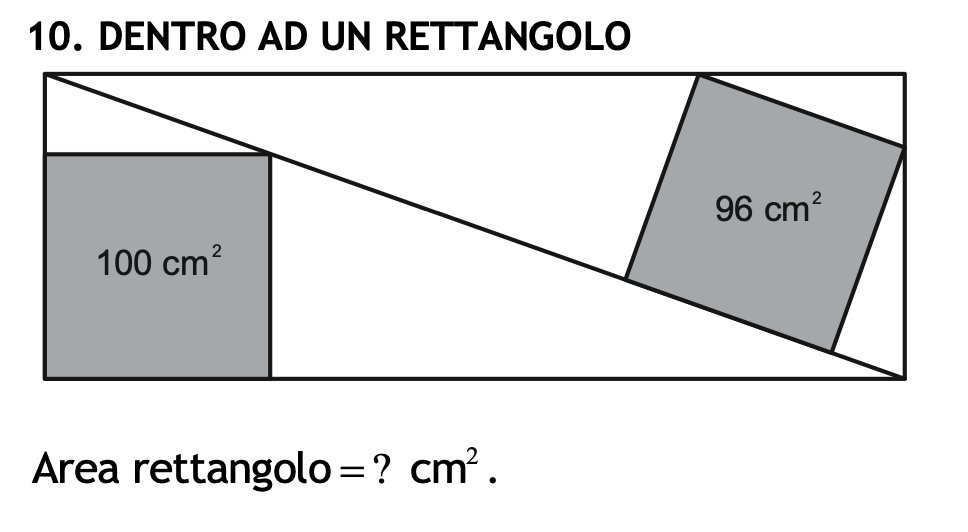
A Problem From Three Days Ago’s Simulation
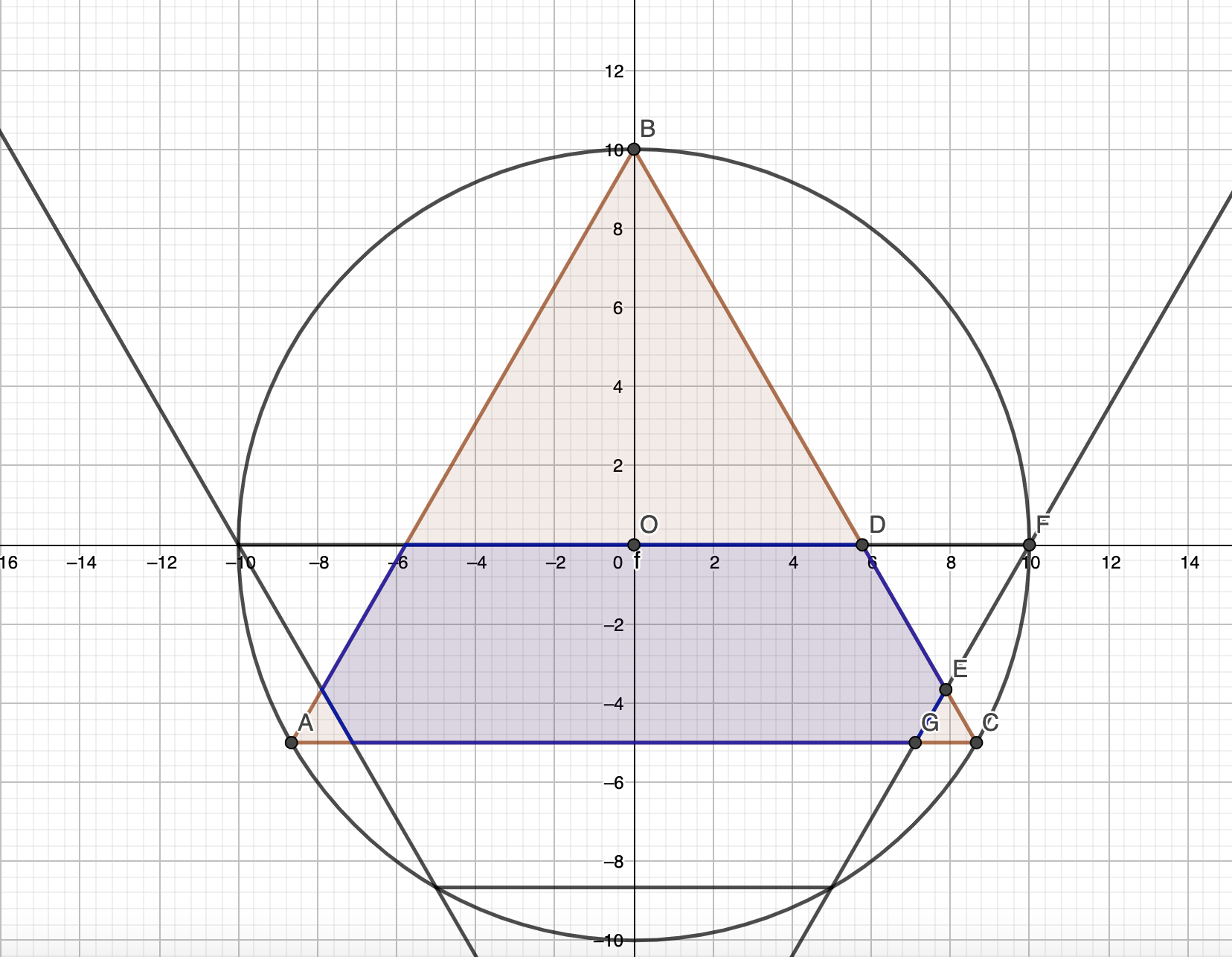
This problem took me a while to solve because of its calculations, but it’s actually very instructive. It makes you see how few conditions can determine a lot. All of the data is in the figure above, we have to find the area of the rectangle. Now let where alpha is the biggest of the […]
Geometry Problem From Today’s Simulation
Today there was a national maths team competition simulation on phiquadro.it and, although I was really on fire, I was really upset I had no time to solve this geometry problem, so I decided to publish it here. In the figure above, the equilateral triangle ABC has circumradius = 10. An isosceles trapezoid is drawn […]
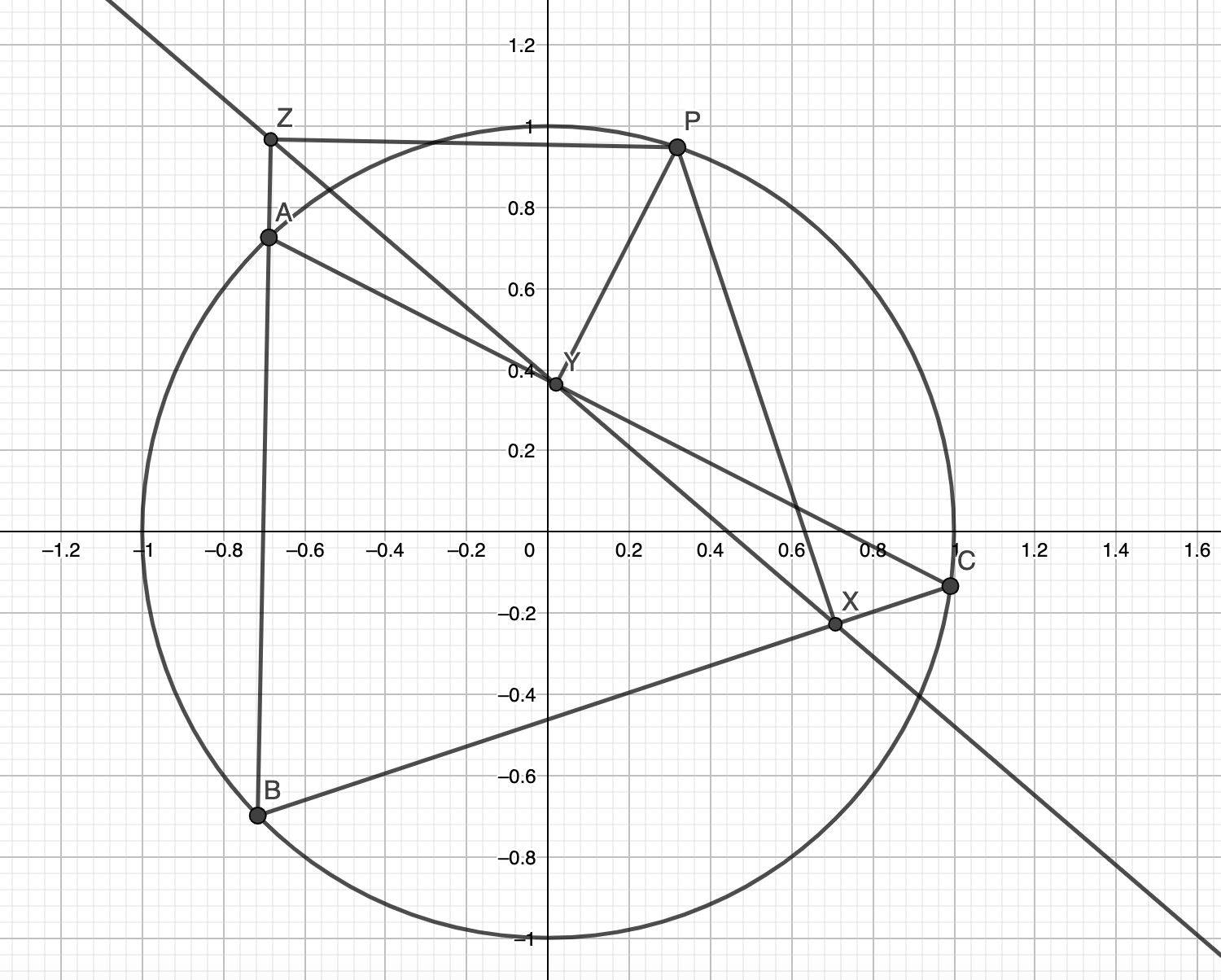
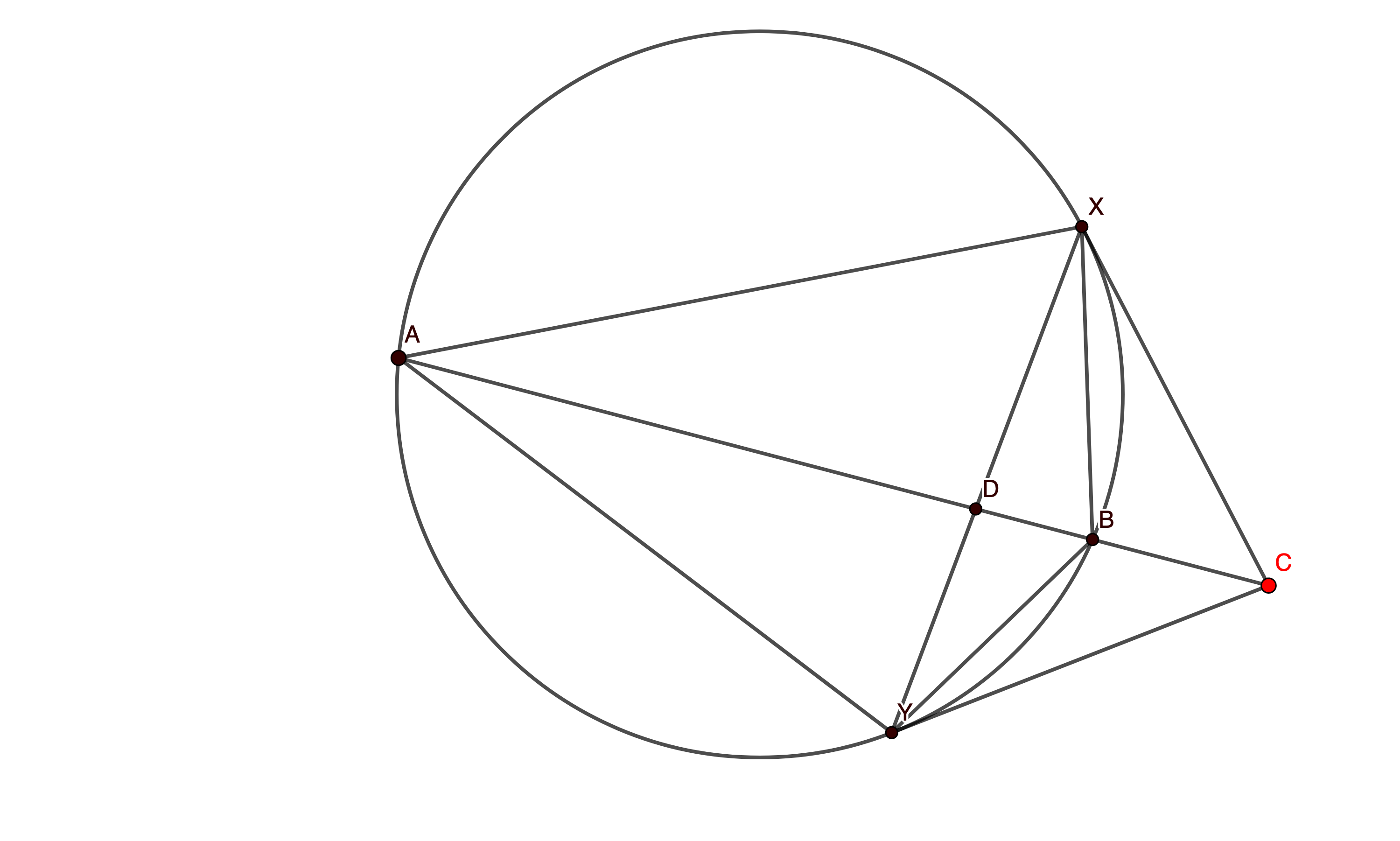
Simson Lines In USA TST
Given a point P on a triangle’s ABC’s circumcircle, then its projections on the sides of ABC are collinear (Simson Line). Using the notation from the figure above, notice that perpendiculars produce cyclic quadrilaterals: P is on the circumcircle of triangles YZA, ZXB and XYC. So we compute: due to all the cyclic quadrilaterals, and […]
Sometimes Geometry Just Needs Smart Calculations
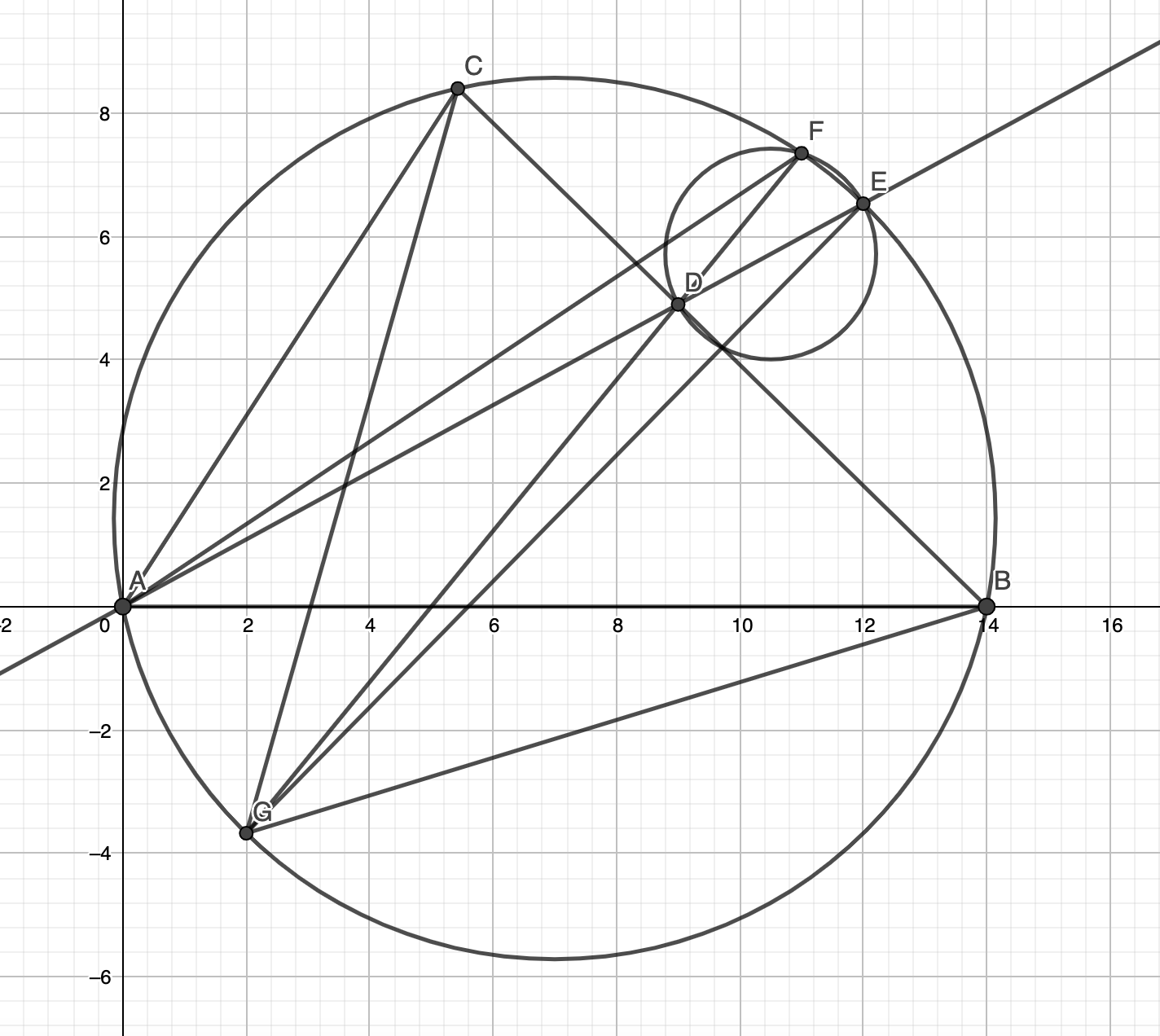
In the figure, suppose AB = 14, BC = 12, CA = 10. AD is the angle bisector of A, intersecting the circumcircle of ABC at E. The circle with diameter DE intersects the circumcircle of ABC again at F. Find the measure of AF squared. To solve this problem, I used a theorem named […]
Ellipses And Dilations
I found this problem in the last phase of a team championship I am participating in. We have an ellipse of equation A line through the origin intercepts the ellipse in two points. We draw the tangents to the ellipse at these points and complete the rectangle in such a way that its sides are […]
An Insight Into Projective Geometry
Projective Geometry is a very nice tool we can employ when we have to work with a lot of intersections and it can even handle intersections on circles. Now let’s gain an insight into its main principles. Oh Cross Ratio, My Cross Ratio A proof involving projective geometry always (and when I say always I […]