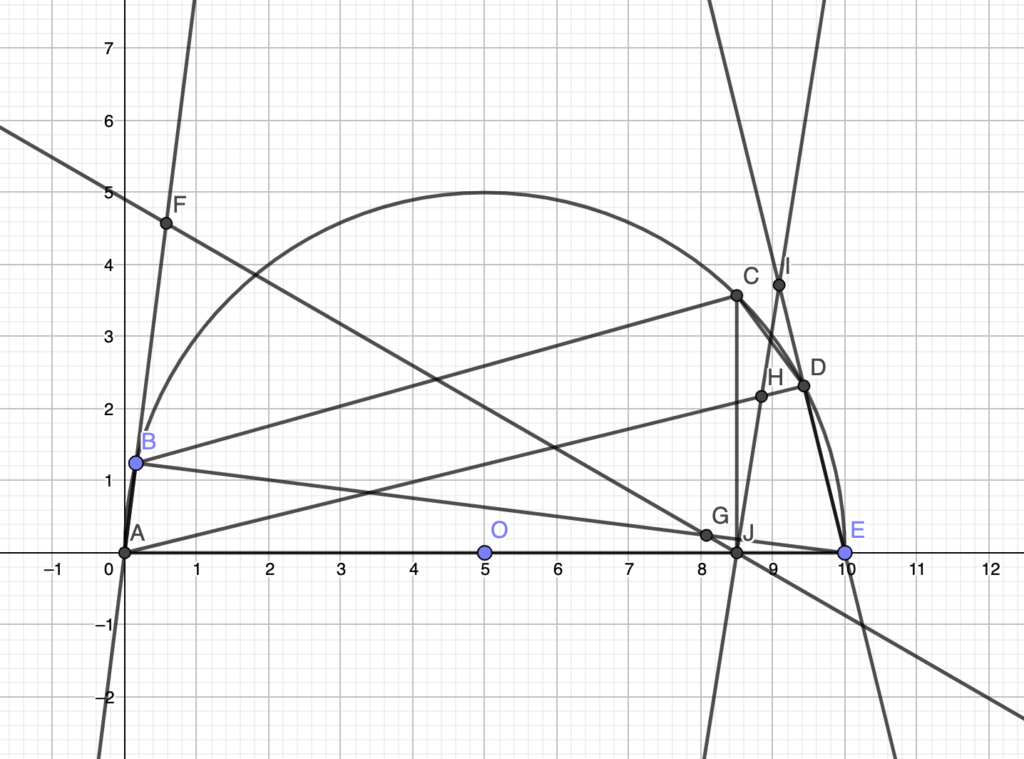
We have a cyclic pentagon, such that AE is a diameter and equals 10. We know and
.
Now F, G, H, I are the feet of the perpendiculars from C to AB, EB, AD, ED. If FG and HI concur at J, find FJI.
Now, let K be the foot of the perpendicular from C to AE. Notice that quadrilaterals CIDH () and CHKA (
) are cyclic. Hence, we get:
This means that H, I, K are collinear. By an analogous reasoning, we get that even F, G, K are collinear.
Hence, FG, HI and AE concur at K, which actually is J.
Now, because AFCJ is cyclic (), we get
.
Similarly, from the ciclicity of CIEJ, we get .
Hence, we deduce .
Because and the radius of the circumference is 5, we conclude (by the sines theorem) that
.
Hence,