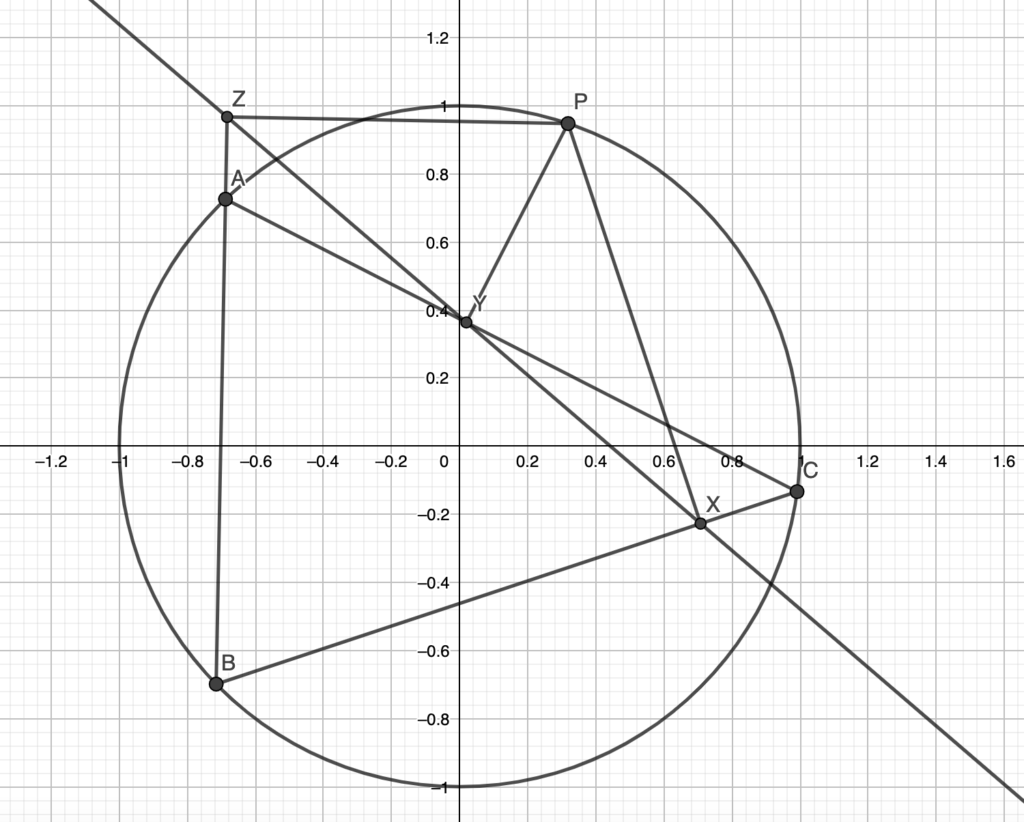
Given a point P on a triangle’s ABC’s circumcircle, then its projections on the sides of ABC are collinear (Simson Line).
Using the notation from the figure above, notice that perpendiculars produce cyclic quadrilaterals: P is on the circumcircle of triangles YZA, ZXB and XYC.
So we compute:
due to all the cyclic quadrilaterals, and we are done.
Problem From USA TST 2014
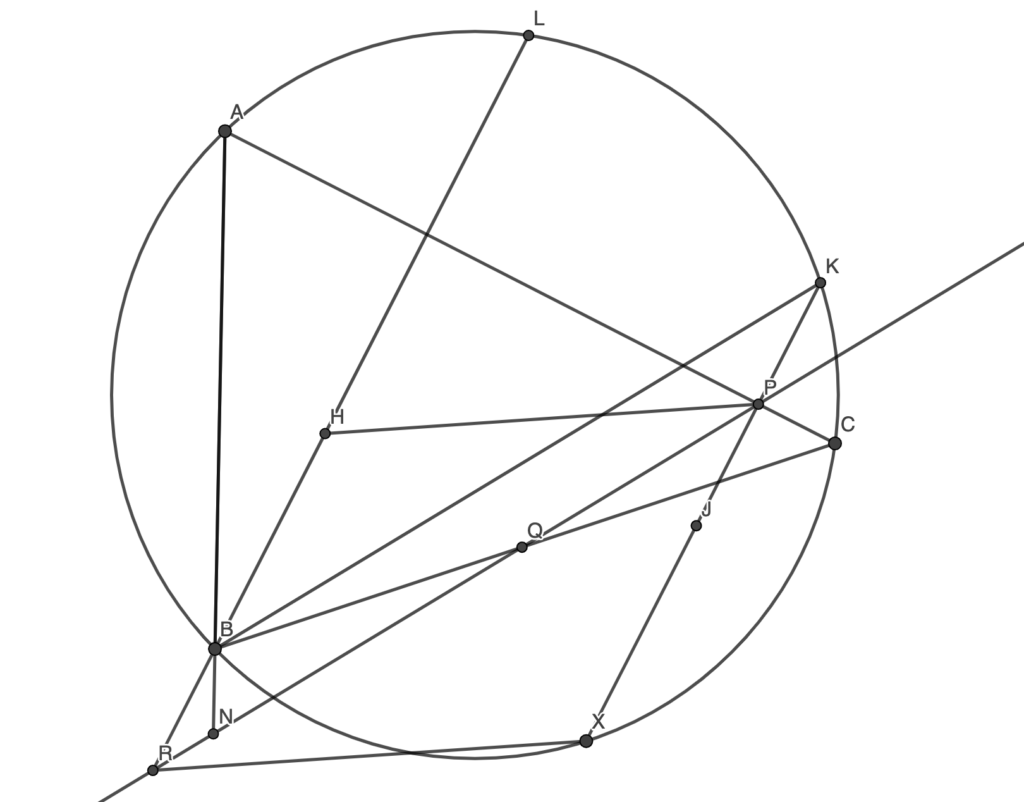
Let ABC be an acute triangle and X be a variable interior point on minor arc BC. Let P and Q be the feet of the perpendiculars from S to lines CA and CB respectively. Let R be the intersection of line PQ and the perpendicular from B to AC. Let y be the line through P parallel to XR. Prove that y always passes through a fixed point.
Seems hard, but let us prove a nice lemma.
Lemma 1: Let H be the orthocenter of ABC, then RHPX is a parallelogram.
Let XP extended meet the circumcircle of ABC at K and let N be the foot of X on AB. Obviously P, Q, N are collinear (Simson Line). Then we see that
Hence RP is parallel to BK. Obviously RB is parallel to PK too, hence RBKP is a parallelogram.
Let J be the reflection of K over AC, then because the reflection of the orthocenter of a triangle over any side lies on its circumcircle and line XK is an altitude of XAC, J is the orthocenter of XAC.
Let L be the reflection of the orthocenter over AC. Then HJKL is an isosceles trapezoid by symmetry, but also BXKL is an isosceles trapezoid since XK is parallel to BL and BXKL is cyclic.
That means BX is parallel to HJ. Obviously BH is parallel to XJ, so BHJX is a parallelogram.
By ‘summing’ the two parallelograms we’ve obtained so far, we see that RHPX is a parallelogram, hence we are done.
Now we go back to our problem.
We know that line y, the parallel through P to RX, always passes through H because RHPX is a parallelogram by Lemma 1, so we are done.
Simson Lines are a very powerful tool in the mathematical olympiads and I recommend to look through the various interesting configurations they generate to have a better sense of what’s really going on.