I found this problem in the last phase of a team championship I am participating in.
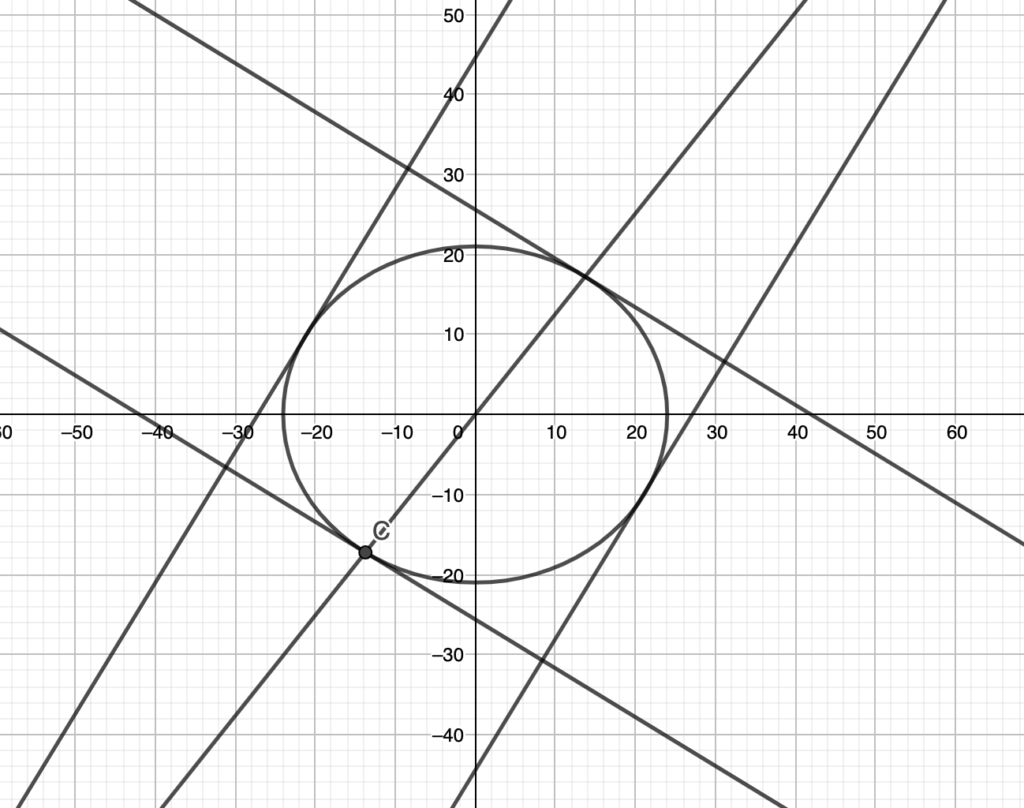
We have an ellipse of equation
A line through the origin intercepts the ellipse in two points. We draw the tangents to the ellipse at these points and complete the rectangle in such a way that its sides are tangent to the ellipse. What’s the area of that rectangle?
Now the brutal method is considering a random line through the origin, intersecting it with the ellipse, computing the equations of the tangent lines and then considering a random set of parallel straight lines, finding the ones that are tangent to the ellipse and finally finding the 4 points of the rectangle.
That’s a waste of time. There’s a simple trick involving dilations which will make life and calculations simple.
A Nice Trick
Now consider the situation in the photo below.
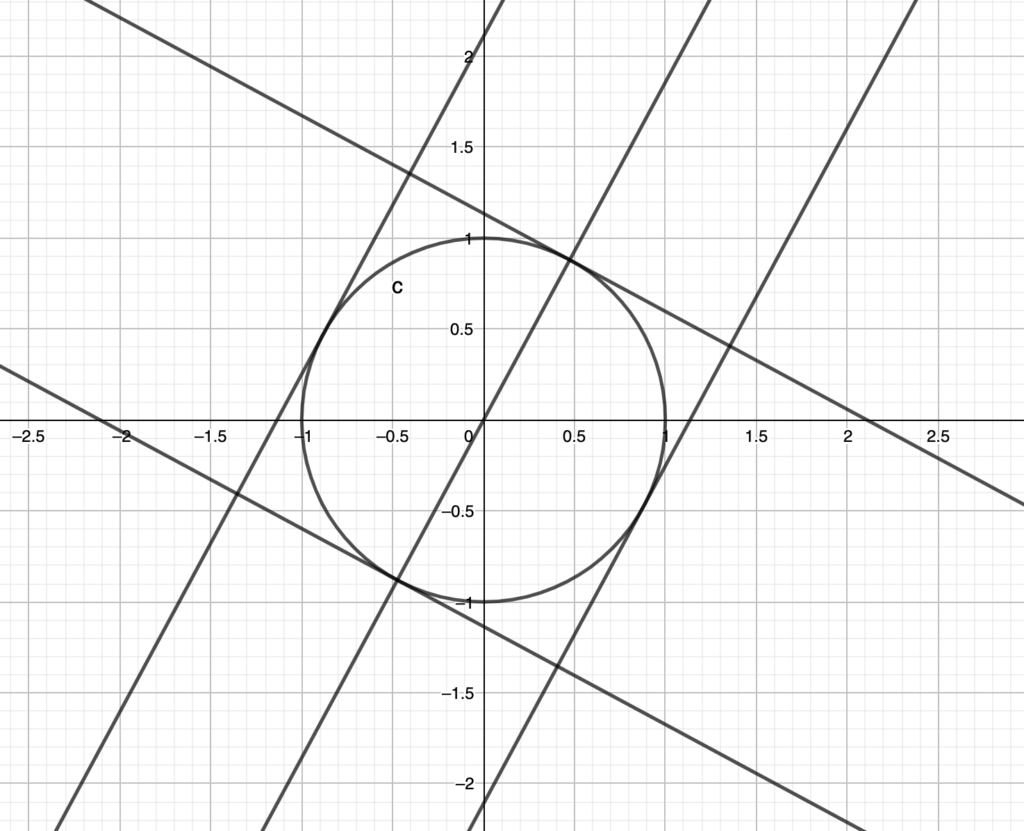
We have a circle with radius equal to 1. We get a random line through the origin and draw the rectangle. It’s easy to see that it’s always a square with side equal to 2.
Now the trick is applying this dilation:
Since dilations preserve intersections, the circle will become our original ellipse and the square a random rectangle.
By the properties of dilations, to find its area we just need to multiply the area of the square for both the dilation coefficients.
So we get that the area equals: