One very famous programming challenge is: given a function which generates a random real number in the interval [0,1], calculate the value of pi. At first glance, it could seem that it could seem that the data and the request are completely different, but with a little math trick we can actually compute the value of pi.
The Idea
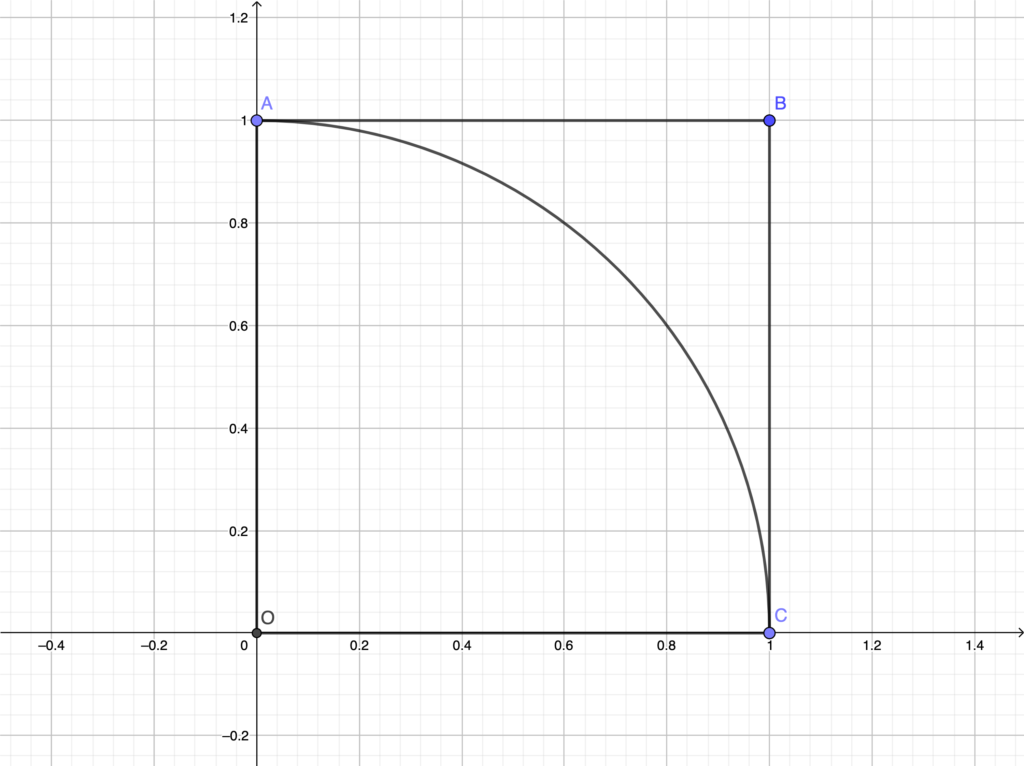
Notice that the square OABC is the region of the plane which contains all the points with x and y coordinates in [0,1], while the circle quarter OAC is the region of the plane with x^2+y^2<=1. So if I take the ratio of such areas I obtain (pi*r^2/4)/r^2 = pi/4 so I can obtain an approximation of pi.
The Program Implementation
import random
precision = 10000000
count = 0
for i in range(0, precision):
if pow(random.uniform(0, 1), 2)+pow(random.uniform(0, 1), 2) <= 1:
count = count + 1
# print count
print 4*float(count)/precision
So what this program does is generating 10000000 random points in OABC and taking the ratio between the ones who are contained in the circular sector and all of them, which can give a nice approximation of pi.
The last output was: 3.1413932.