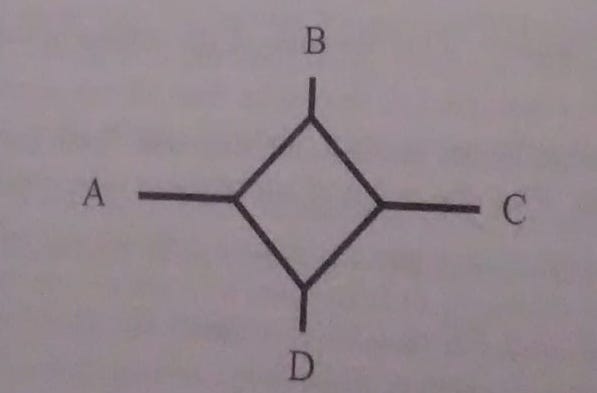
A Problem From Stanford Mathematics Tournament 2008 (Team Test)

Daphne is in a maze of tunnels shown below. She enters at A, and at each intersection, chooses a direction randomly (including possibly turning around). Once Daphne reaches an exit, she will not return into the tunnels. What is the probability that she will exit at A?

The Idea

At first, I will denote by $p(A), p(C)$ the probabilities that Daphne will exit the maze respectively at A, C. Let’s suppose Daphne just doesn’t turn around and exit the maze (which occurs with a probability of $\frac{1}{3}$ ), in this case she will either find herself on the intersections that bring to B or D. It’s very easy to notice the symmetry: in this case the probability that she will exit the maze from A is equal to the probability that she will exit the maze from C. So we can write the equality: $p(A) = p(C) + \frac{1}{3}$ .

Other Useful Observations

Let’s call “move” when Daphne decides the direction to follow in one of the intersections. Let’s colour the intersections that bring to A and C white and the other black. Moving from a white intersection can result in exiting the maze or going into a black intersection and vice versa. This means that the parity of the moves needed to reach a black intersection is opposite to the parity of the moves needed to reach a white intersection. When Daphne starts at A, she makes a move and either exits the maze or goes into a black intersection. So when Daphne arrives to a black intersection she has already made an odd number of moves and, to exit the maze, she needs one more move. Hence we deduce that if Daphne takes exactly makes 2n moves to exit the maze, then she is at B or D. Obviously this implies that if she exits the maze from A or C, she has made an odd number of moves.

We also see that at any moment, the probability of exiting the maze is $\frac{1}{3}$ and the probability of not exiting the maze is $\frac{2}{3}$ .