Geometry Problem From Today’s Simulation – Mattia Giuri's bizarre blog

Today there was a national maths team competition simulation on phiquadro.it and, although I was really on fire, I was really upset I had no time to solve this geometry problem, so I decided to publish it here.

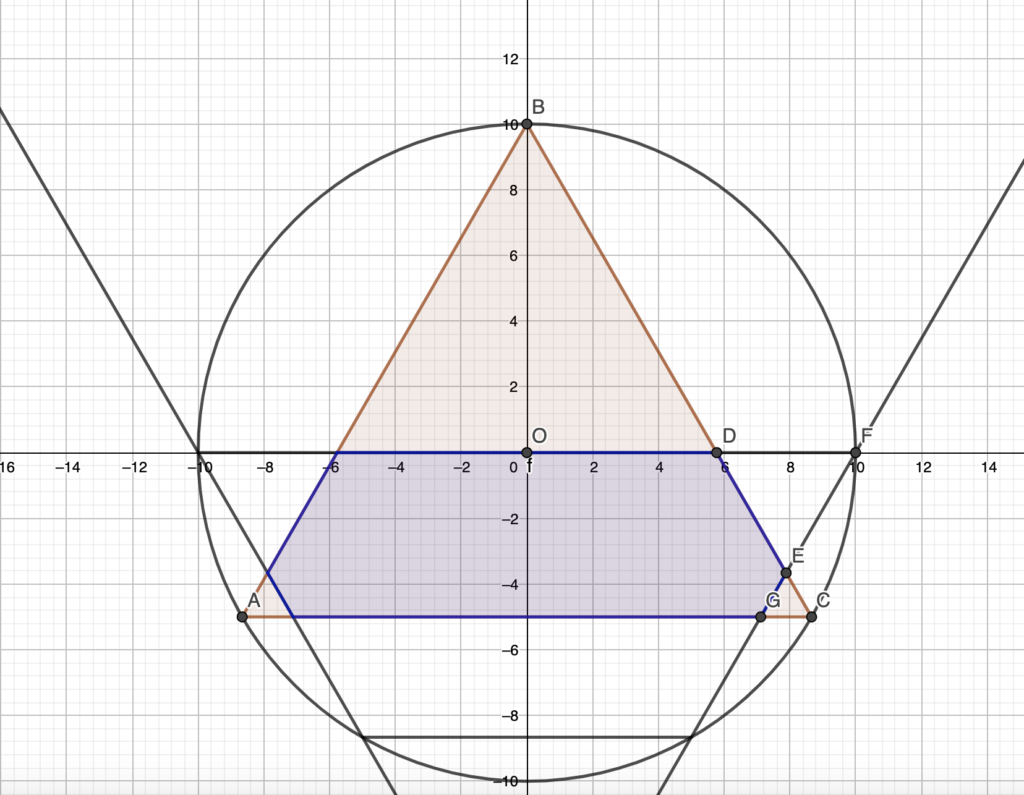
In the figure above, the equilateral triangle ABC has circumradius = 10. An isosceles trapezoid is drawn with base on the diameter and oblique sides parallel to the triangle’s sides. Find the value of the blue area.

Now let $BD = a, DE = b, EC = c$ . The side of the equilateral triangle equals $\frac{3}{2}10\frac{2}{\sqrt{3}} = 10\sqrt{3}$ .

So $a+b+c = 10\sqrt{3}$ .

Also, since DEF is equilateral and $BO=OF=10$ , we have $\frac{a}{2} + b = 10$ .

But we actually know $a$ because of Thales Theorem: it equals $\frac{2}{3}10\sqrt{3} = \frac{20\sqrt{3}}{3}$

So $b = 10-\frac{10\sqrt{3}}{3}$ and $c = 10\sqrt{3}-a-b=\frac{20\sqrt{3}-30}{3}$

So now, since also ECG is equilateral, the blue area equals the area of the big triangle minus the area of triangle with side a minus 2 times the area of triangle with side c:

$\frac{\sqrt{3}}{4}(300- a^2 -2c^2) = 25(8-3\sqrt{3})$

The problem requested an approximation of 100 times the area, which equals

$7009$