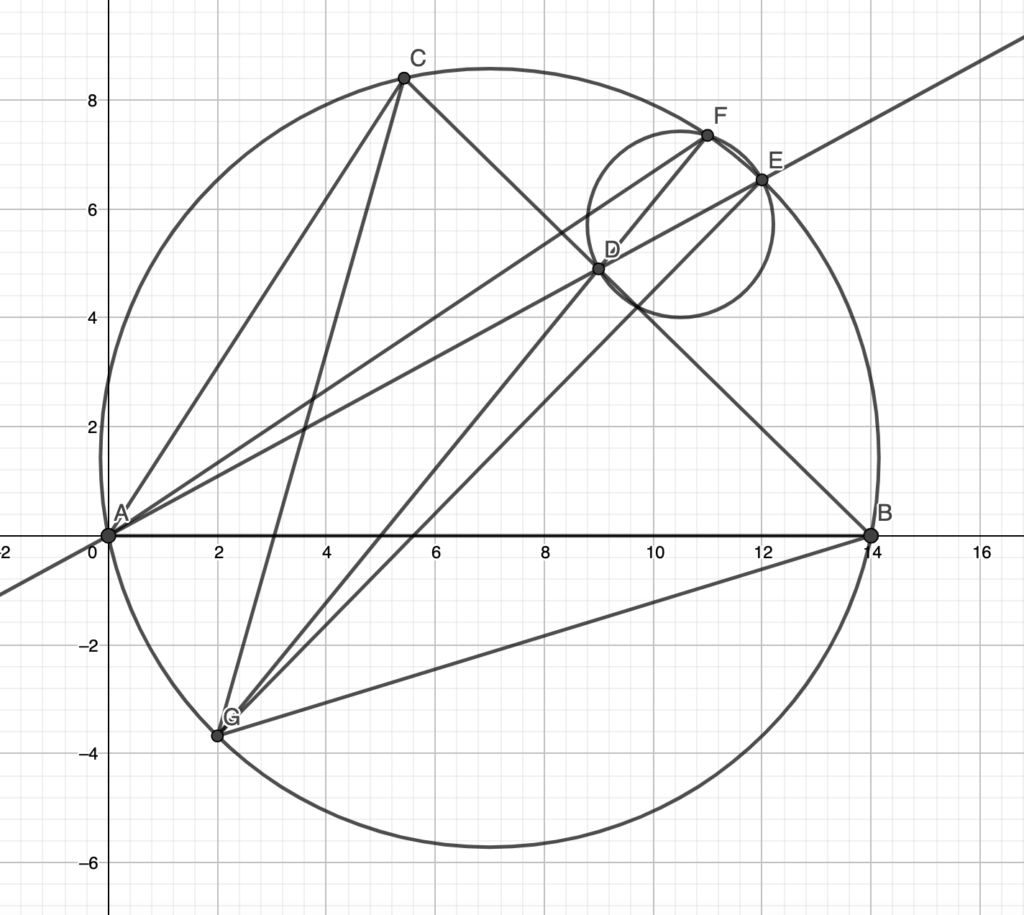
Sometimes Geometry Just Needs Smart Calculations

In the figure, suppose AB = 14, BC = 12, CA = 10. AD is the angle bisector of A, intersecting the circumcircle of ABC at E. The circle with diameter DE intersects the circumcircle of ABC again at F. Find the measure of AF squared.

To solve this problem, I used a theorem named Stewart’s Theorem, I’ll provide its proof in this article below.

Stewart’s Theorem

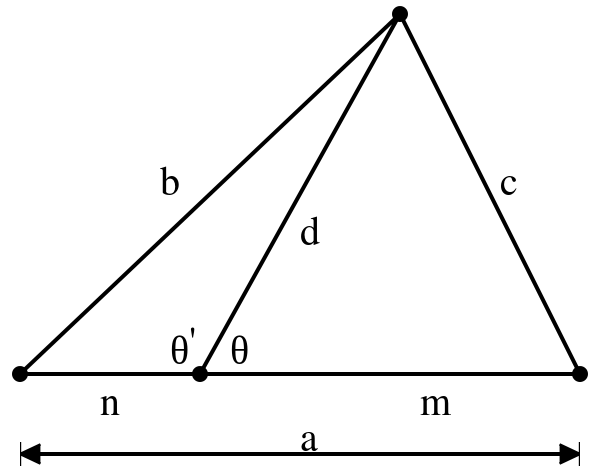
Referring to the figure above, Stewart’s Theorem says:

$b^2m+c^2n = a(d^2+mn)$

To prove it, notice that by Carnot’s Theorem:

$c^2 = m^2 + d^2 -2md\cos{\theta}$

$b^2 = n^2 + d^2 -2nd\cos{\theta'} = n^2 + d^2 + 2nd\cos{\theta}$

Using these relations we get:

$b^2m + c^2n = m^2n+mn^2 + (m+n)d^2 = (m+n)(d^2+mn) = a(d^2+mn)$

And we are done.

Back To Our Problem

Now let G be the diametrically opposite of E, then obviously G,D,F are collinear since $\widehat{GFE} = \widehat{DFE} = \frac{\pi}{2}$

Notice quadrilateral GEFA is cyclic, so triangles GED and AFD are similar, and we get:

$\frac{AD}{DG} = \frac{AF}{GE}$

Hence

$\frac{AD^2}{DG^2} = \frac{AF^2}{GE^2}$

Now by the Bisector’s Theorem we know

$\frac{BD}{DC} = \frac{AB}{CA}$

So BD = 7, DC = 5.

Now, by Stewart’s Theorem on triangle ABC, we get:

$AD^2 = \frac{10^2 \cdot 7 + 14^2 \cdot 5}{12} -35 = 105$

By Carnot’s Theorem, we have:

$\cos{CAB} = \frac{14^2+10^2-12^2}{2 \cdot 10 \cdot 14} = \frac{19}{35}$

$\sin{CAB} = \sqrt{1 - \cos{CAB}^2} = \frac{12\sqrt{6}}{35}$

By the Law of Sines, we get

$GE^2 = (\frac{BC}{\sin{CAB}})^2 = 1225/6$

Now, since AE is the angle bisector of CAB, we know E is the midpoint of minor arc BC, so its diametrically opposite B must be the midpoint of major arc BC, hence CG = BG.

Now, by Carnot’s Theorem, we get

$CG^2 = \frac{12^2}{2(1-\frac{19}{35})} = \frac{315}{2}$

Hence, by Stewart’s Theorem:

$DG^2 = \frac{315}{2} - 35 = \frac{245}{2}$

Finally, using our initial relation we get

$AF^2 = \frac{105 \cdot \frac{1225}{6}}{\frac{245}{2}} = 175$