Writing a sudoku solver is a great example to show how recursion works in Python. This particular technique is called ‘Backtracking’. Let’s see a possible implementation.
How Sudoku Works
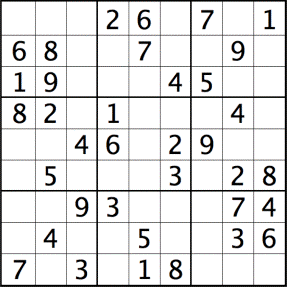
There are 3 rules you have to follow when solving a sudoku:
- All the numbers in a row must be different;
- All the numbers in a column must be different;
- All the numbers in one of the 9 highlighted 3X3 squares must be different.
So this means that at each step we’ll have to check whether it’s possible to put a number into a certain empty box.
Code Implementation
Let’s start to see some code now. At first we transfer our sudoku into a Python-readable numpy array.
import numpy as np
sudoku = np.array([ [0,0,0,2,6,0,7,0,1],
[6,8,0,0,7,0,0,9,0],
[1,9,0,0,0,4,5,0,0],
[8,2,0,1,0,0,0,4,0],
[0,0,4,6,0,2,9,0,0],
[0,5,0,0,0,3,0,2,8],
[0,0,9,3,0,0,0,7,4],
[0,4,0,0,5,0,0,3,6],
[7,0,3,0,1,8,0,0,0]]
)
You can see that it’s the exact copy of the photo above. Now let’s see the checker.
def checker(x, y, n):
global sudoku
# checks row and column
for i in range(9):
if (sudoku[y][i] == n) or (sudoku[i][x] == n):
return False
# checks the square
xi = (x // 3) * 3
yi = (y // 3) * 3
for i in range(3):
for j in range(3):
if sudoku[yi + i][xi + j] == n:
return False
return True
To access a box in column x and row y we need to call sudoku[y][x]. Also, remember a numpy array is 0-indexed, which means that its first element has index 0. The values of xi and yi represent the box which is found in the lower left corner of each of the nine squares. So our checker will return True if it’s possible to put the number n in the box with coordinates (x, y).
Now the fun begins. We’re ready to write the solver:
def solver():
global sudoku
for y in range(9):
for x in range(9):
if sudoku[y][x] == 0:
for n in range(1, 10):
if checker(x, y, n):
sudoku[y][x] = n
solver()
sudoku[y][x] = 0
return
print(sudoku)
input('Find more solutions if exist')
This program finds each empty box, puts a number in it and then calls itself again until the puzzle is completed. If no numbers can be put in an empty box, the ‘return’ allows to go one recursive step back and continue from there.
Notice that we’re working on the global variable sudoku. If we tried to pass sudoku into the function as a parameter, then the recursive trick wouldn’t work. In fact, by doing so we’re directly working on the same variable without creating any copy of it that would eventually blow up after a recursive step.
[[4 3 5 2 6 9 7 8 1]
[6 8 2 5 7 1 4 9 3]
[1 9 7 8 3 4 5 6 2]
[8 2 6 1 9 5 3 4 7]
[3 7 4 6 8 2 9 1 5]
[9 5 1 7 4 3 6 2 8]
[5 1 9 3 2 6 8 7 4]
[2 4 8 9 5 7 1 3 6]
[7 6 3 4 1 8 2 5 9]]
Here’s a solution. Anyway, let’s say we have more than one solution. Then, the code would print all of them at once. The last line of code allows you to see them one by one. You just need to press ‘Enter’ to make the code keep going after one solution (if found). Let’s try to remove a couple of numbers from our sudoku to see the result.
sudoku = np.array([ [0,0,0,2,6,0,7,0,1],
[6,8,0,0,7,0,0,9,0],
[1,9,0,0,0,4,5,0,0],
[8,2,0,1,0,0,0,4,0],
[0,0,4,6,0,2,9,0,0],
[0,5,0,0,0,3,0,2,8],
[0,0,9,3,0,0,0,7,4],
[0,4,0,0,5,0,0,3,6],
[7,0,3,0,0,0,0,0,0]]
)
So the numbers 1 and 8 were removed from the last row.
[[4 3 5 2 6 9 7 8 1]
[6 8 2 5 7 1 4 9 3]
[1 9 7 8 3 4 5 6 2]
[8 2 6 1 9 5 3 4 7]
[3 7 4 6 8 2 9 1 5]
[9 5 1 7 4 3 6 2 8]
[5 1 9 3 2 6 8 7 4]
[2 4 8 9 5 7 1 3 6]
[7 6 3 4 1 8 2 5 9]]
Find more solutions if exist
[[4 3 5 2 6 9 7 8 1]
[6 8 2 5 7 1 4 9 3]
[1 9 7 8 3 4 5 6 2]
[8 2 6 1 9 5 3 4 7]
[3 7 4 6 8 2 9 1 5]
[9 5 1 7 4 3 6 2 8]
[5 6 9 3 1 8 2 7 4]
[2 4 8 9 5 7 1 3 6]
[7 1 3 4 2 6 8 5 9]]
Find more solutions if exist
Process finished with exit code 0
Nice. But now let’s make an easier to use version.
Class SudokuSolver
import numpy as np
class SudokuSolver:
def __init__(self, sudoku):
self.start_sudoku = sudoku
self.sudoku = sudoku
self.solutions = {}
self.counter = 0
self.solver()
def checker(self, x, y, n):
# checks row and column
for i in range(9):
if (self.sudoku[y][i] == n) or (self.sudoku[i][x] == n):
return False
# checks the square
xi = (x // 3) * 3
yi = (y // 3) * 3
for i in range(3):
for j in range(3):
if self.sudoku[yi + i][xi + j] == n:
return False
return True
def solver(self):
for y in range(9):
for x in range(9):
if self.sudoku[y][x] == 0:
for n in range(1, 10):
if self.checker(x, y, n):
self.sudoku[y][x] = n
self.solver()
self.sudoku[y][x] = 0
return
# print(self.sudoku)
self.counter = self.counter + 1
self.solutions[self.counter] = self.sudoku
# input('Find more solutions if exist')
def all_solutions(self):
return self.solutions
sudoku = np.array([ [0,0,0,2,6,0,7,0,1],
[6,8,0,0,7,0,0,9,0],
[1,9,0,0,0,4,5,0,0],
[8,2,0,1,0,0,0,4,0],
[0,0,4,6,0,2,9,0,0],
[0,5,0,0,0,3,0,2,8],
[0,0,9,3,0,0,0,7,4],
[0,4,0,0,5,0,0,3,6],
[7,0,3,0,0,0,0,0,0]]
)
sudoku_master = SudokuSolver(sudoku)
sudoku_solutions = sudoku_master.all_solutions()
# print(sudoku_solutions)
# print(sudoku_master.start_sudoku)
This way you’ll have all of your solutions nicely collected in a dictionary as well as the initial sudoku stored in a private variable.