An Insight Into Projective Geometry – Mattia Giuri's bizarre blog

Projective Geometry is a very nice tool we can employ when we have to work with a lot of intersections and it can even handle intersections on circles. Now let’s gain an insight into its main principles.

Oh Cross Ratio, My Cross Ratio

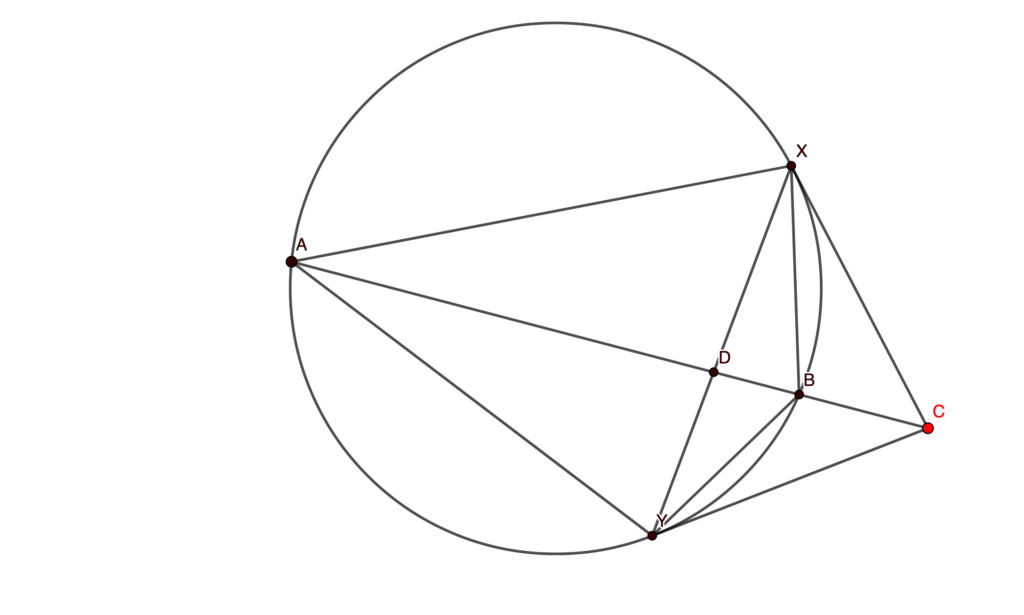
A proof involving projective geometry always (and when I say always I mean in every single proof) involves the Cross Ratio: in Figure 3 it’s $\frac{AX}{XB}\frac{BY}{YA}$ , and we indicate it with $(A,B;X,Y)$ . Warning: $(A,B;X,Y)$ is different from $(B,A;X,Y)$ . That’s because it’s this type of writing which indicates the Cross Ratio we want to consider, so if you want to use it in your proofs, remember to write the right form of the Cross Ratio. But why is this entity so good?

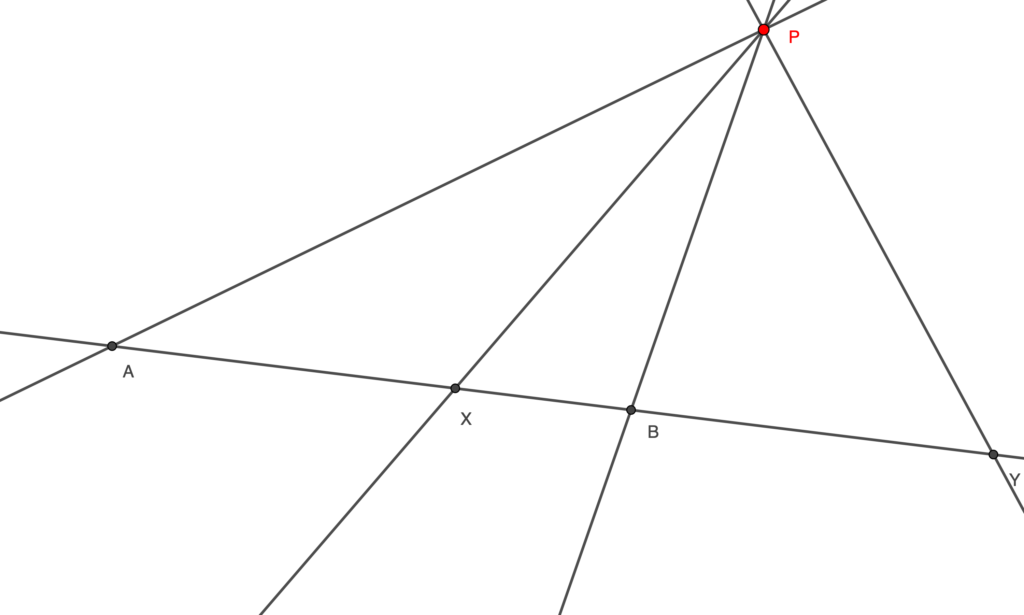
Constant Cross Ratio

The interesting thing is that if we have, say, four lines passing through a point $P$ and we cut them as in the picture with another line $r$ , the Cross Ratio does does not depend on the choice of $r$ .
It can be easily proved by law of sines, writing $AX = \frac{PX\sin(APX)}{\sin(PAX)}$ , $XB = \frac{PX\sin(XPB)}{\sin(PBX)}$ , $BY = \frac{PY\sin(BPY)}{\sin(PBY)}$ , $AY = \frac{PY\sin(APX)}{\sin(APY)}$ .

And we obtain that the Cross Ratio is equal to
$\frac{\frac{PX\sin(APX)}{\sin(PAX)}}{\frac{PX\sin(XPB)}{\sin(PBX)}}$ $\frac{\frac{PY\sin(BPY)}{\sin(PBY)}}{\frac{PY\sin(APY)}{\sin(PAY)}}$ .

So everything turns into $\frac{\sin(APX)}{\sin(XPB)}\frac{\sin(BPY)}{\sin(APY)}$ since in a cyclic quadrilateral opposite angles add up to $\pi$ and $\sin{(x)} = \sin{(\pi - x)}$ , clearly independent from the choice of $r$ .
Cross Ratio can be negative because we consider directed lenghts. In fact, what catches our attention are Harmonic Bundles: Cross Ratios such that $(A,B;X,Y) = -1$ . So the Idea of all of the projective problems is to switch from a line to another one keeping the Cross Ratio constant, process which we will refer to as taking perspectivity at a point P.

Cross Ratios in Circles

When points P,A,B,X,Y are concyclic, the Cross Ratio is also constant. The proof is even easier than before, in fact we just write $AX = 2R\sin(APX)$ , $XB = 2R \sin(XPB)$ , $BY = 2R \sin(BPY)$ , $YA = 2R \sin(APY)$ . and we get $(A,B;X,Y) = \frac{2R\sin(APX)}{2R \sin(XPB)} \frac{2R \sin(BPY)}{2R \sin(APY)} \Rightarrow (A,B;X,Y) =\frac{\sin(APX)}{\sin(XPB)}\frac{\sin(BPY)}{\sin(APY)}$ , as foretold.

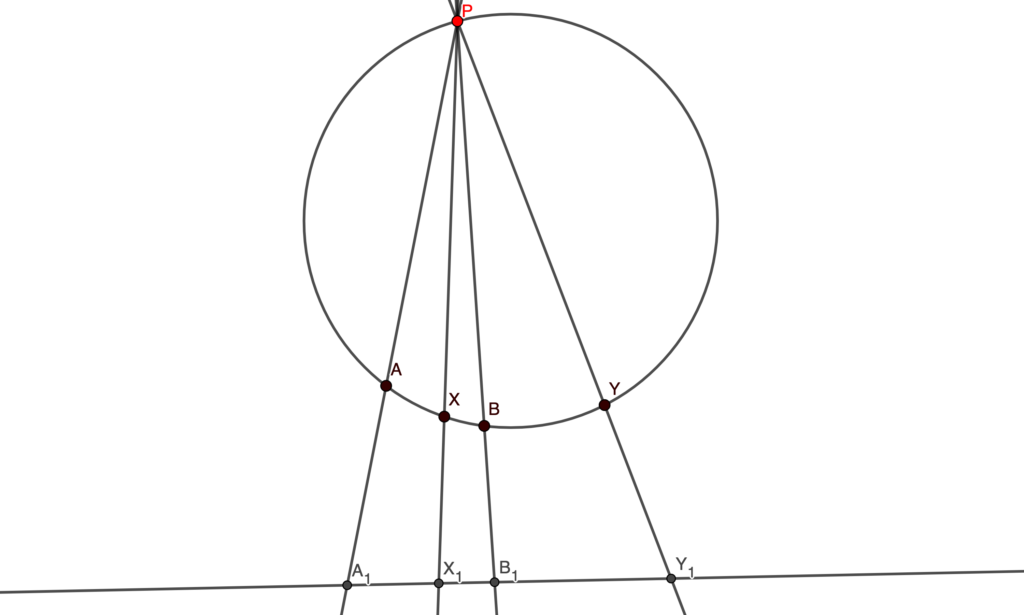
Figure 2: Cross Ratio From Circles To Lines.

Points At Infinity

The points at infinity are imaginary points which are the intersections of parallel lines. It may seem a bit oakward to consider Points at Infinity but reality is that we need them. For example, if we want an Harmonic Bundle with two points $A,B$ and their middle point $M$ , we’ll need to include a Point at Infinity $P_\infty$ .
So we get that $(A,B;M,P_\infty) = -1$ . Points at Infinity can be projected by considering them the intersection of the parallel lines, so they can slide into either of the lines.

Harmonic Quadrilaterals

Harmonic Quadrilaterals are a special type of quadrilaterals which satisfy $(A,B;X,Y) = -1$ .

The characteristic of these quadrilaterals is that if we draw the tangents to the circle at two opposite points, then the intersection of the two tangents and the other two verticles are collinear. How do we prove that such configuration induces an Harmonic Quadrilateral?
Notice that $AC$ is the A-Symmedian (isogonal conjugate of the Median) of $AXY$ by definition, so, by the properties of Symmedians $\frac{AX}{XB}=\frac{AY}{YB}$ . This is enough to force the condition.
Also, $(A,B;D,C) = -1$ . We can prove it by taking perspectivity at point $X$ onto line $AB$ : $A$ and $B$ don’t move, $Y$ becomes $D$ . But how about $X$ ? To project it , we’ll have to consider the tangent at $X$ to the circle, that’s because if we consider a point $Z$ on the circle getting closer and closer to $X$ , the line $XZ$ will become more and more similar to the tangent at $X$ until $Z \equiv X$ , so $X$ becomes $C$ and we are done.